As figuras e formas da natureza podem ser compreendidas como produtos do movimento. O movimento do elemento geométrico mais simples - o ponto - gera linhas e, particularmente, retas. O movimento de segmentos de reta num plano forma figuras planas - retângulos, quadrados, círculos. Já o movimento de figuras no espaço gera corpos. Entre estes últimos, existem alguns muito especiais: são os corpos que se formam a partir do movimento completo de uma figura invariável em torno de um eixo. Este movimento particular recebe o nome de revolução e os corpos por ele gerados são chamados corpos de revolução, que estão presentes de inúmeras maneiras em nossa vida cotidiana.
O Cilindro
 |
| Figura 1 |
| Partindo de um retângulo, fazendo-o girar uma volta inteira sobre um de seus lados. Este lado é o eixo de rotaçãoe corresponde à sua altura, isto é, à distância entre as duas bases do cilindro (Figura 1). |
 |
| Figura 2 |
O lado paralelo ao eixo de rotação será a geratriz do cilindro e adotará infinitas posições. Os outros lados do retângulo são os raios das bases.
| ' | Partindo de uma chapa de forma retangular, vamos enrolá-la sobre si mesma, fazendo com que os dois lados opostos coincidam. Desse modo, observamos claramente que a superfície lateral do cilindro é um retângulo e que as bases são círculos (Figura 2). |
A superfície lateral de um cilindro é obtida partindo-se da planificação do cilindro.
Observe que, no caso da superfície lateral do cilindro, a planificação corresponde a um retângulo. O lado maior do retângulo é proporcional ao comprimento da circunferência e o lado menor do retângulo corresponde à altura do cilindro. Assim, calculamos a sua área lateral a partir da fórmula da área de um retângulo - o produto do comprimento da circunferência da base pela altura:
onde h é a altura e 2 r é o comprimento da circunferência.
r é o comprimento da circunferência.
A área total do cilindro é igual à área lateral mais a área das duas bases (círculos):
 |
Vídeo-Aula:
Achando Volume por integração:
Cone:
O cone é um tipo de forma piramidal. A equação fundamental para pirâmides, um terço vezes base de altitude vezes, aplica-se a cones também.
No entanto, utilizando o cálculo, o volume de um cone é o integrante de um número infinito de infinitamente pequenas placas circulares de espessura dx . O cálculo do volume de um cone de altura h , cuja base está centrado em (0,0,0) com um raio r , é o seguinte.
O raio de cada laje circular é r se x = 0 e 0 se x = h , e variando de forma linear entre, isto é, 

A área da superfície da laje circular é então 

O volume do cone pode ser então calculada como 

e depois da extracção das constantes: 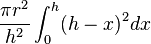
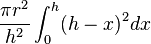
Integrando nos dá 








0 comentários:
Postar um comentário